Límites y Continuidades

Origen:

Unión de dos vocablos que tienen su origen etimológico en lenguas antiguas. Así, límites procede de la palabra latina limes, que es el genitivo de limitis que puede traducirse como borde o frontera de algo.

El límite de una función es el concepto principal que distingue al cálculo del algebra y de la geometría analítica. La noción es fundamental para el estudio del cálculo, ya que analiza el comportamiento de una función cuando la variable toma valores cercanos a un determinado valor del dominio.

Ejemplo:

Limite Finito e Infinito

Limite Infinito:Limx - a f(x)=b <=> para todo ε>0 existe δ>0 / para todo x,0 < |x-a| < δ|f(x) – b| < ε.

Otra notación: Limx->af(x)=b <=> para todo E_b,ε existe un E^*_a,δ / para todo x perteneciente al E^*_a,δ f(x) pertenece a E_b,ε.

Se dice que la función f(x) tiene límite b, cuando x tiende a a, si dado ε positivo arbitrario y tan pequeño como se quiera, existe un δ tal que para todo x perteneciente al entorno reducido de a de radio δ, la función pertenece al entorno de b de radio ε.

Dicho de otro modo, para cualquier número positivo ε, por pequeño que sea, podemos encontrar un δ tal que para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) está dentro del entorno de b de radio ε.

lim x->a f(x)=b significa que por más pequeño que sea el entorno considerado alrededor de b, va a ser posible encontrar un entorno de a, para cuyos valores x(x ≠ a), la función f da como resultado valores que están dentro del entorno de b considerado.

En otras palabras, la función f(x) tiene límite b, cuando x tiende a a, si el valor de la función f(x) se hace arbitrariamente próximo al valor b cuando x se aproxima al valor a.

Límites infinitos

Empecemos definiendo qué es un límite infinito de una función f(x):limx→+∞f(x)=+∞⟺ dado un número arbitrario k, existe otro número h tal que si x>h entonces f(x)>k

Intuitivamente, nos viene a decir que podemos conseguir que f(x) sea tan grande como queramos sólo escogiendo un valor suficientemente grande de x.

Para límites donde x tiende a menos infinito: limx→−∞f(x)=+∞⟺ dado un número arbitrario k, existe otro número h tal que si x<−h entonces f(x)>k

limx→−∞f(x)=−∞⟺ dado un número arbitrario k, existe otro número h tal que si x<−h entonces f(x)<−k

Caso 1: lim_x->af(x) = +inf <=> para todo A > 0 existe δ > 0 para todo x perteneciente al E^*_a,δf(x) > A.

En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.

Caso 2:lim_x->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δf(x) < -A.

Caso 3:lim_x->+inff(x) = +inf <=> para todoA > 0 existeB > 0 / para todox > Bf(x) > A.

Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.
Caso 4: lim_x->+inff(x) = -inf <=> para todoA > 0 existeB > 0 / para todox > Bf(x) < -A.

Caso 5:lim_x->-inff(x) = +inf <=> para todoA > 0 existeB > 0 / para todox < -Bf(x) > A.

Caso 6:lim_x->-inff(x) = -inf <=> para todoA < 0 existeB < 0 / para todox < -Bf(x) < -A.

Caso 7:lim_x->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x > B f(x) pertenece al E_b,ε.

Caso 8:lim_x->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x < -B f(x) pertenece al E_b,ε.

Continuidad en un Punto

El término continuo aplicado a una función de variable real sugiere que su gráfica no debe presentar saltos; es decir, que al trazar su gráfica no se requiera alzar la mano. Sin embargo se hace necesario formalizar matemáticamente esta definición

Teorema de Continuidad

Ejercicio:  Resuelva el siente ejercicio planteado

Continuidad en un Intervalo

Continuidad de una función en un intervalo abierto

 Una función es continua en un intervalo abierto o unión de intervalos abiertos si es continua en cada punto de ese conjunto.

Decimos que f(x) es continua en (a, b) sí y sólo sí f(x) es continua " x Î (a, b).

Ejemplo: La función m: R  ®  R / m(x) =  es continua en los intervalos (-¥ , 2) È (2, +¥).

  
Su gráfica:

Ejercicio: Analice la continuidad de la función h(x) =  en el intervalo (–1, 1).

Continuidad de una función en un intervalo cerrado

La continuidad de una función en un intervalo cerrado [a, b] no es sencilla de analizar como en el caso de intervalos abiertos. Dado que al considerar el intervalo cerrado [a, b] la función no está definida a la izquierda de a como tampoco a la derecha de b, no tiene sentido considerar los límites en a y en b. Esto hace que no se pueda definir la continuidad en esos dos puntos. Se debe definir primero la continuidad por derecha y la continuidad por izquierda en un punto.

Definición. Una función es continua a la derecha de un número a si   y es continua a la izquierda de a si  .

Ejemplo: La función que describe el radio (en metros) del flujo circular de petróleo que se derrama por una fisura de un tanque luego de t minutos está dada por:    

Su gráfica:



Ejercicio:
Sea la función f(x)= x² + 1. ¿Se puede afirmar que la función toma todos los valores del intervalo [1,5]?

Propiedades de los límites

Ejercicio: Calcular el siguiente limite, justificando que propiedad esta usando.

Aplicación de los límites en la arquitectura

Los límites en la Arquitectura,  sirven para la  elaboración de gráficas que ayudan a saber el nivel de producción y  encontrar el menor costo posible para generar una mayor ganancia; es decir un análisis financiero.

Un ejemplo de esto es cuando se presenta un alza en los costos del material o que costo se había generado anteriormente, además nos ayuda a saber qué precio que se aplicara al nuevo diseño arquitectónico para el futuro cliente.

Se usan los  límites en el cálculo (análisis de lo real y matemático) para definir convergencia, continuidad, derivación, integración de muchas cosas.

También sirve para realizar cálculos estructurales de un puente o una edificación a futuro.

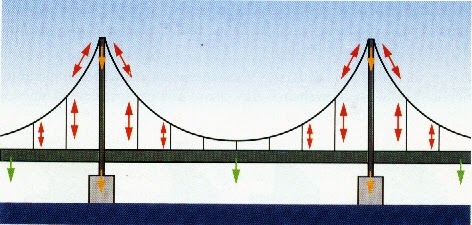
 Otra aplicación de los límites es saber el crecimiento de una población en la cual se va a trabajar; y el trabajo que éste desempeñará, al construir una vivienda más por cada habitante que se integre, y poder calcular más o menos un balance total.

Continuidad de un intervalo en la Arquitectura:

• Estructuras de vigas columnas, losas
• Deformaciones de vigas
  

En la arquitectura se  tiene en cuenta los límites ya que ayudan a  resolver los problemas que ellos generan, mediante soluciones.

Video:

Bibliografia: 

• http://electrodragones.wordpress.com/limites-finitos-y-limites-infinitos/
• http://ed21.webcindario.com/LimitesYContinuidad/limites_unilaterales.htm
• https://www.dspace.espol.edu.ec/bitstream/123456789/781/2/1486.pdf
• http://www.fca.unl.edu.ar/Continuidad/3.2%20Funci%F3n%20continua%20en%20unintervalo.htm
• http://www.vitutor.com/fun/3/c_a.html
• http://matematica.50webs.com/limite-infinito.html