Secciones Cónicas

´

Se denomina sección cónica a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

Etimología

La primera definición conocida de sección cónica surge en la Antigua Grecia, cerca del año 1000 a.C (Menæchmus) donde las definieron como secciones «de un cono circular recto». Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Perge

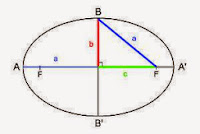
Elipse:

Una elipse es el conjunto de todos los puntos de un plano cuya suma de distancias a dos puntos fijos es una constante..

El uso de las  elipses en la arquitectura se encuentra en construcciones de anfiteatros, escaleras caracol cuyo cañón tiene forma de elipse.

Ejercicio:

Escribe la ecuación reducida de la elipse que pasa por el punto (2, 1) y cuyo eje menor mide 4.

Anfiteatro de Pompeya

Parábola:

Curva abierta formada por dos líneas o    ramas simétricas respecto de un eje y en que todos sus puntos están a la misma distancia del foco  y de la directriz 

La parábola tiene importancia en la arquitectura, ya que la misma tiene resistencia estructural y estética, la utilizan en arcos, cúpulas, puentes, etc.

Ejercicio:

Determina la ecuación de la parábola que tiene por directriz la recta: y= 0 y por foco el punto (2, 4).

Puente sobre el Sena

Coliseo Romano

Hipérbole:

La hipérbola es aquella curva plana y simétrica respecto de dos planos perpendiculares entre sí, mientras que la distancia en relación a dos puntos o   focos resulta constante.

 Es el lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos llamados focos siempre es constante y menor que la distancia entre los focos.  Se las puede  encontrar en estructuras de soporte, cubiertas, como columnas y torres y chimeneas, etc. 


Ejercicio:

El eje principal de una hipérbola mide 12, y la curva pasa por el punto P(8, 14). Hallar su ecuación.

Catedral de Brasilia

Circunferencia:

La línea cerrada de formato curvo y apariencia plana en la cual los puntos resultan equidistantes del punto central que se localiza en el mismo plano. Esta distancia que separa al conjunto de puntos y al área central se conoce como radio, mientras que el segmento de recta que compone un par de radios alineados recibe el nombre de diámetro.

En el uso de la circunferencia produce un ahorro de espacio en superficies, comportamiento adecuando frente a la radiación solar y los vientos, aumento de la eficiencia energética, pues brinda gran facilidad a la hora construir.

La circunferencia se utiliza a menudo en escaleras de espiral, estadios, cúpulas, teatros, adornos, etc.

Ejercicio: 

Los extremos del diámetro de una circunferencia son los puntos A(−5, 3) y B(3, 1). ¿Cuál es la ecuación de esta circunferencia?

Palacio Nacional da Pena-Sindra (Portugal)

Aplicación de las cónicas en la Arquitectura

Desde tiempos inmemorables los arquitectos se basaron en abstraer figuras geométricas para la aplicación en sus diseños. Es por tal razón que se da uso a las cónicas en la arquitectura.

Al evolucionar la arquitectura, los materiales, la tecnología, 
las edificaciones construidas mostraba y muestran el uso de las cónicas, que dan realce a la obra, permitiendo dar un goce estético que caracteriza al profesional en esta rama.

Las construcciones modernas también nos permiten observar el uso de las cónicas, estando presentes en los puentes, en el ámbito estructural, peso; también presentes en cúpulas en el variando de la estructura y función; también en escaleras y balcones y en diferentes partes de una edificación, se podrá apreciar las cónicas. 

Videos:

Matrices

El elemento integrado o “material” que genera comunicación virtual en la arquitectura lo denominaríamos “matriz”. La “matriz” depende de su relación con el entorno, del edificio o espacio donde se integra, así como de las visuales y de la superficie aparente que puede generar, de las diferentes posiciones del observador y de su propia definición de imagen, generalmente baja. Depende de la arquitectura, de su morfología y de su escala, de la conformación del espacio urbano y del papel que desarrolla en él.

Así mismo si entendemos visualmente el Paisaje como el espacio que ingresa en el campo visual humano, con características morfológicas similares en función de una escala y una localización; y que el  Paisaje Urbano es la secuencia de espacios y elementos relacionados percibidos en serie, resultantes de la actividad humana directa o indirecta, que configuran el espacio público, permiten la vida social y dotan de significado a la urbe.

Tipos de matrices en la Arquitectura

• Matriz de Relaciones

La matriz Es una representación gráfica que permite descubrir cualquier tipo de relación deseada entre actividades, por medio de ejes cartesianos que se prolongan y forman una retícula, sobre la cual se vacían los datos deducidos.
es una retícula en 2 dimensiones compuesta por números o datos colocados en líneas o columnas.

• Matriz de interrelación

Consiste en ver las zonas del programa arquitectónico y ver sus relaciones ya sea directo, indirecto y nulo.

• Matriz de rigidez de una estructura

Se presenta el aula de la matriz de rigidez de dos formas: Primera trabajando  con toda la matriz de compatibilidad de deformaciones y la segunda calculando con las submatrices de la matriz  A.

Bibliografía:

http://www.espe.edu.ec/portal/files/libros/analisis/capi10p.pdf

http://es.slideshare.net/LuisSoto32/diagramacion-en-arquitectura

http://www.buenastareas.com/ensayos/Matriz-Arquitectura/7421866.html

http://mateunfv.blogspot.com/